Tosa's twaddlin' tavern
go back to homepage
Here I'll publish primarily english-language articles and explanations, but I might publish something in italian when I feel like it. The topics can be anything I want since who cares, but I'll probably talk about guitar, maths, physics and books. I might publish photos of the stuff I build or of my plants.
|

|
05/09/2024| The Golden Ratio, or, How Broccoli are keeping a Secret from You (work in progress)
back to top
Ever since humanity emerged from its cradle in the scorching savannas of South Africa, the pursuit of beauty has driven generations of artists to paint their works, musicians to compose, craftsmen to sharpen their skills, writers to paint the world through poetry and philosophers to- well, to do whatever they're doing.
Through the meandering rivers and cultivated plains of the Fertile Crescent and in the miriad of islands of the Aegean, the art of mathematics developed alongside human culture. One might discuss for days what the "true" subject of mathematical enquiry is, but it is an undisputable fact that some people find a simple and satisfying beauty in proofs and shapes. While it is true that maths and geometry developed at first with the intent of measuring the countryside and counting sheep, their continous advancements were later fuelled by a desire to uncover more and more of its intricacies and wonders.

It is only natural then that because of this fascination with the hidden beauty of maths several experts tried to reduce beauty to a single mathematical entity. Ancient Greek and Hellenic mathematicians noticed that a number often appeared in several geometrical figures, be it in the ratio between a regular pentagon's diagonal and one of its sides, or between the length of the side of a pentagram and the side of the internal pentagon; they called it φ (phi). It is first defined in Euclid's "Elements", with the rather convoluted:
"A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser."
Now, you may think that this phrase is particularly incomprehensible, and you'd be perfectly right, but consider that maths up until around the time of Descartes used to be done like this: through words, like philosophical logic. When greek authors discuss quadratic equations, they're not talking about equations containing x to the power of 2, they're straight up talking about a square with side of length x. In simpler, modern algebraic form, φ is defined as follows:
Visually, this can be seen like this, where a + b is to a as a is to b:
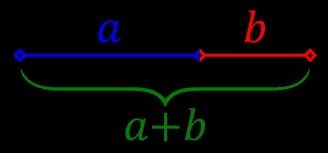
Do take note of the fact that a and b can be any length you like, as long as both of those lengths' ratio is the golden ratio. If it isn't, then the equation above isn't solvable.
One particular property that confused pythagoreans a lot was phi's irrationality (I'll make a quick explainer on irrationality sooner or later. Put simply, irrational numbers have infinitely many decimal numbers, without any pattern to them, like pi or Napier's number. They're a pretty weird lot and have many interesting properties and stories, ranging from hellenistic cults to the development of the first supercomputers.). To pythagoreans, numbers were limited to positive integers, and all the numbers inbetween were represented by fractions of those same positive integers. How can you have a negative length? A negative area? How can a number that comes before a finite number be infinite? That would mean that there are infinitely many small jumps between 1 and 2, that's ridiculous! Infinite new numbers, contained between the confines of the two tiniest numbers... This was the story that pi and phi, along with square roots, revealed to those early, ancient mathematicians. They opened our minds to countless new realms, and by filling the gaps on the number line they opened wider ones in our minds.
That's all well and good you might say, but what's all that got to do with beauty? Well, before going into this, let's have a short break. Take a few deep breaths, stare away from your computer, go for a walk, reread passages that weren't clear to you. Done? Very good, now look at this broccoli:

Isn't it beautiful? No? Well you ain't either so shut up and listen to what I'm about to say: this misterious vegetable has a secret second life. During the day, it's a stinky ingredient in a lot of stews and pies, but during the night, when no one is watching (or smelling, because man this veggie has a godawful stench) it becomes an abstract mathematical entity, made up of spirals and infinite structures. This very broccoli is a perfect example of a natural fractal. What's a fractal? It's a wonderfully weird part of mathematics. To explain them, we'll have to go down a couple of dimensions.
Did you see that?!?! That was a single point. One minuscule dot. An infinitely small portion of space. No, it wasn't a speck of dust on your screen, it's all in your head, it's a mathematical abstraction of something that in reality doesn't really exist. An idealism.